Determining the Field of View of Coaxial Lighting
Figure 1 shows a cross-section of a Coaxial Light. Light from the LED is reflected using a half-mirror, so that the position of the emitting surface can be treated as if it were directly behind the mirror (See “Virtual emitting surface” in the figure). In this case, the distance from the emitting surface to the workpiece is LWD'.
The effective field of view of a Coaxial Light is determined by 1) the LWD (distance from the Light Unit to the workpiece) and 2) the WD (distance from the workpiece to the camera). Figure 2 shows how to determine the field of view "V" when the WD is held constant and the LWD (distance to the Light Unit) is varied. The following is an explanation of what the effective field of view will be when the virtual emitting surface is at positions A and B.
In the case of position A, if we assume that the workpiece is a reflecting surface, we can say that there is an emitting surface at A opposite to the workpiece (position A' of the LWD'a distance). Therefore, when the workpiece is viewed through the camera, it appears as if the emitting surface is at A', and thus the effective field of view is Va.
In the same way, in the case of B, the emitting surface is at B' and the effective field of view is Vb. Comparing Va to Vb, we find that Va, which has a shorter LWD, has a greater effective field of view. In this way, the effective field of view grows larger as the LWD becomes smaller.
What is the effective field of view?
For example, when reading characters engraved on a shiny piece of metal, if we assume that the virtual emitting surface is at position B, the effective field of view of Vb will be determined, in regards to the camera field of view V as shown in Figure 3 below, by the virtual emitting surface position B'. For this reason, only the letters CDEFG will be visible as dark letters against a light background, and the letters AB and HI, which appear dark against a dark background, will not be discernible. In this way, the effective field of view Vb is smaller than the field of view V.
Figure 1. Cross-section of Coaxial Light
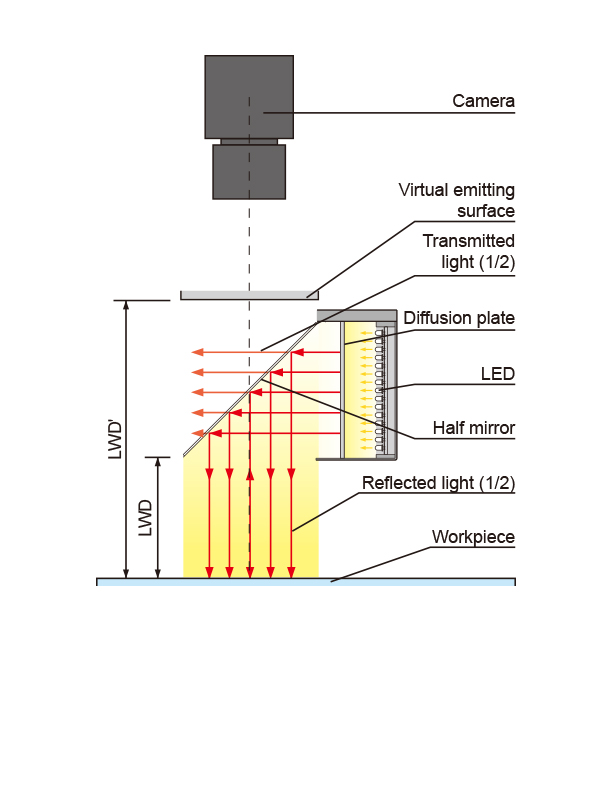
Figure 2. Determining the field of view by LWD
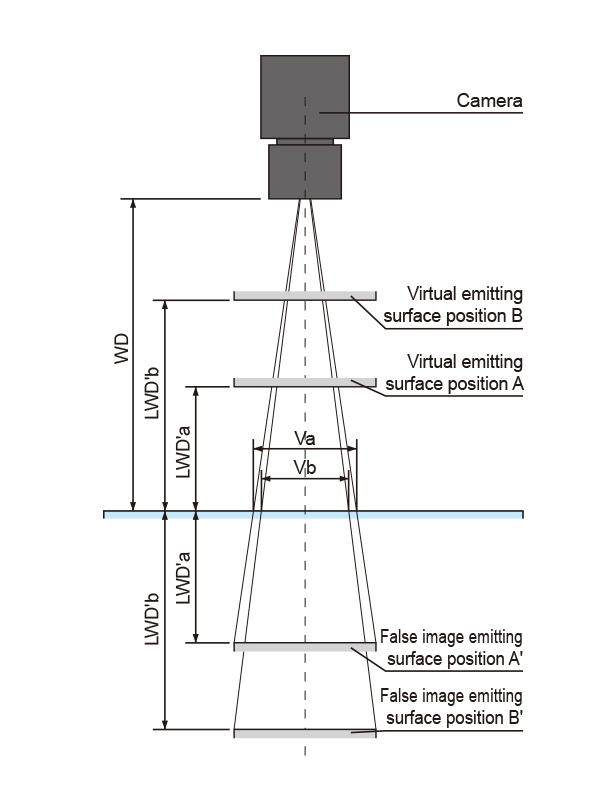
Figure 3. Field of view and effective field of view


